Page 65 - 111-1閱讀心得作品集_完整版

從一題多解看數學學習歷程
肆、研究分析與結果

一、多邊形對角線斜率解法

令推導多邊形時以 ( )為其中一邊，上下兩側個別能繪出一個正多邊形。
̅

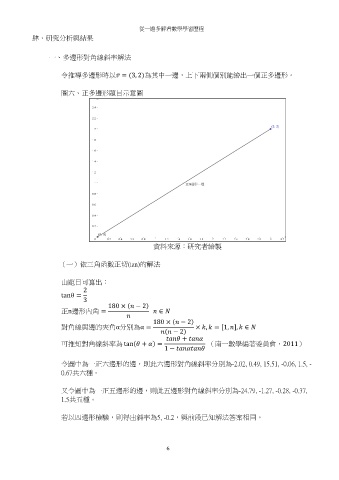
圖六、正多邊形題目示意圖

資料來源：研究者繪製

（一）依三角函數正切(tan)的解法

由題目可算出：

( )
正 邊形內角

( )
對角線與邊的夾角 分別為 [ ]
( )

可推知對角線斜率為 ( ) （南一數學編著委員會， ）

令圖中為一正六邊形的邊，則此六邊形對角線斜率分別為-2.02, 0.49, 15.51, -0.06, 1.5, -
0.67共六種。

又令圖中為一正五邊形的邊，則此五邊形對角線斜率分別為-24.79, -1.27, -0.28, -0.37,
1.5共五種。

若以四邊形檢驗，則得出斜率為5, -0.2，與前段已知解法答案相同。

6