Page 105 - 107-11071115梯次小論文比賽得獎作品

正三角形任意折時形成的重疊面積
2 4
0 < <
3 + √3 (√3 + )(1 + √3 )

因而計算出 m=-1 或 m≥1。因為形成四邊形時斜率必須大於零所以 m=-1
不合。由以上推導我們可以知道在任何一個大於 1 的斜率時，其 Q 點在
2
2 √3+3 √3(1+ )
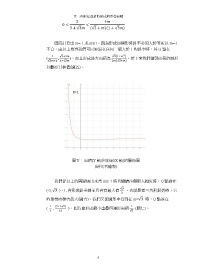
( , )，而且形成最大面積為 。接下來我們繪製面積的圖形
√3 +3 3+√3 2 (√3+ )
以觀察其極值(圖五)。

X=1

圖五：面積(Y 軸)與斜率(X 軸)的關係圖

(研究者繪製)

我們從以上的圖歸納出來當 m≥ 1 時且繼續往無限大趨近時，Q 點會在

√3
( 0, √3 )，L 會形成鉛垂線並且會有最大值 ，也就是當三角形對折時，它
2
的重疊面積會最大(圖六)。我們又從圖形中得到在 m=√3 時，Q 點落在

1
1
( , (3+4√3) )，此時會形成最小重疊四邊形面積 (圖七)。
3 13 √3

6