Page 107 - 107-11071115梯次小論文比賽得獎作品
P. 107
正三角形任意折時形成的重疊面積
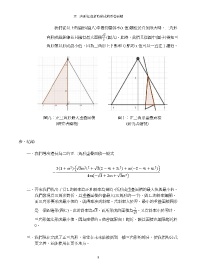
我們從以上的圖形(圖八)中看到當斜率(x 值)趨近於負無限大時,三角形
√3
會形成鉛錘線並且擁有最大面積 (圖九)。此時,我們又從圖中(圖十)得知三
2
角形難以形成最小值,因為三角形上 P 點和 Q 點的 x 值可以一直往 1 趨近。
圖九:正三角形最大重疊面積 圖十:正三角形重疊面積
(研究者繪製) (研究者繪製)
參、結論
一、我們導出邊長為二的正三角形重疊面積一般式
2
2
2
2 2
3(1 + m ) (√3m t + √3(2 − 4t + 3t ) + m(−2 − 4t + 6t ))
−
2
4m(−√3 + 2m + √3m )
二、 再來我們找出了當L的斜率為正和斜率為負時,所形成重疊面積的最大值與最小值。
我們發現當三角形對折,其重疊面積值會最大(三角形的一半),與 L 的斜率無關。
而三角形要形成最小值時,就得牽涉到斜率。當斜率大於零,最小的重疊面積圖形
1
是一個四邊形(圖七)。此時斜率為√3,而所形成的面積為 。又當斜率小於零時,
√3
三角形無法形成最小值。因為座標的 x 值會無限向 1 趨近,讓其面積也無限趨近於
0。
三、我們現在完成了正三角形,希望在未來能推廣到一般三角形的部分,使我們的公式
更完善,並能使用在更多地方。
8