Page 11 - 1090325小論文

解析工業的血液：以數據分析與人文地理探討元大石油指數趨勢圖

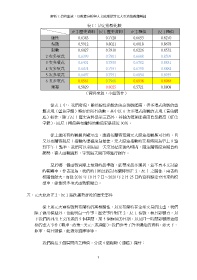
表 1：決定係數比較
正 2 歷史資料 反 1 歷史資料 正 2 極值 反 1 極值

線性 0.6383 0.7728 0.6653 0.8270
指數 0.5912 0.8021 0.6018 0.8678
對數 0.6027 0.7810 0.6226 0.8532
2 次多項式 0.6399 0.7801 0.6688 0.8599

3 次多項式 0.6401 0.7890 0.6782 0.8831
4 次多項式 0.6474 0.7951 0.6790 0.8884
5 次多項式 0.6497 0.7951 0.6854 0.8959

6 次多項式 0.6561 0.7966 0.6938 0.8984
乘冪 0.5829 0.8025 0.5721 0.8808
（資料來源：小組製作）

從表 1 中，我們發現：雖然線性函數的決定係數頗高，但多項式函數的整
體表現（藍色字體）略好於所有函數。其中以 6 次多項式函數的表現（黃色網
底）較佳，除了反 1 歷史資料是第三高外，其餘的預測準確度皆是最高（紅色

字體），而反 1 極值與布蘭特的數值更是接近 90％。

從上述所有的數據皆顯示出，透過布蘭特預測元大原油指數是可行的，且
又以布蘭特對反 1 指數的準確度為最佳。元大原油指數的交易時間為早上 9 點
到下午 1 點半，我們可以利用前一天交易結束後的時間，關注蘭特原油期貨的

趨勢，套入函數圖形，等到隔天開市時進行操作。

至於哪一個函數實際上預測的最準確，能帶來最多獲利，並不再本文討論

的範疇中。作者認為，我們的目的是探討布蘭特與正 2、反 1 之關係：兩者的
相關性頗大，而從 2016 年 10 月 7 日～2020 年 2 月 25 日的資料點建立出來的模
型中，線性與多項式函數較擬合。

五、元大原油正 2、反 1 漲跌趨勢背後的歷史事件

從上述元大兩指數對布蘭特的高相關性，以及布蘭特在全球交易的比重，我們
除了做出模型外，也能明白一件事：歷史事件對正 2、反 1 指數，極具影響力。以

下我們將列出上文所述的 9 個區間，前 5 個極值的日期，以及同一時間影響原油價
格的重大事件（戰爭、政策、美元、或通膨）。我們參考了許多網站的資料，如天下、
鉅亨、每日頭條、能源知識庫等等。

我們將這 5 個區間內之極值，分成 4 個趨勢（漲幅）探討：

7