Page 99 - 小論文作品集封面側標-1080331

Sigma 與空間相遇的地方

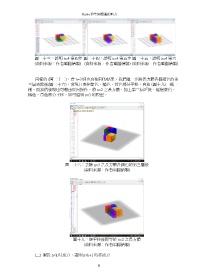
圖二十三：證明 n=4 第四步 圖二十四：證明 n=4 第五步 圖二十五：證明 n=4 第六
(資料來源：作者電腦繪製) (資料來源：作者電腦繪製) (資料來源：作者電腦繪製)

同樣的 (圖二十二)，當 n=3 時也有相同的結果。我們進一步將長方體各個顏色的第
三層去除後(圖二十六)，發現只要把紫色、橘色、黃色部分平移，會和 (圖十九)一模一
2
樣。而我們發現也可藉由反向操作，將 n=2 之長方體，加上第三層3 後，經過紫色、
橘色、黃色部分平移，即可證明 n=3 的模型。

圖二十六：去除 n=3 之長方體各顏色的第三層後
(資料來源：作者電腦繪製)

圖十九：經平移後即等於 n=2 之長方體
(資料來源：作者電腦繪製)

(三) 假設 n=k 時成立，證明 n=k+1 時亦成立

6